Acomodando números
¡Armemos un rompecabezas!
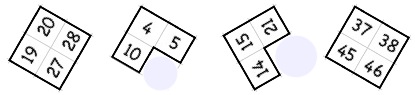
Este problema ha sido diseñado para trabajarse en grupos de cuatro (más o menos).
Vea las "Notas para los maestros" para mayor información.
Hay dos rompecabezas que puede imprimir desde esta liga.
1. Complete cada rompecabezas y luego ponga las piezas en los cuadrados
marcados en la figura de abajo, que se pueden imprimir de aquí
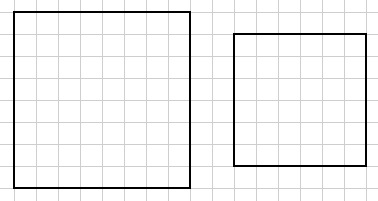
2. Ponga el cuadrado pequeño con números encima del cuadrado grande
como usted desee, pero tal que las cuadrículas se empalmen. (Puede ser
más fácil copiar los números del cuadrado pequeño en una hoja transparente).
3. Explore qué pasa si suma los números que aparecen uno encima del otro.
4. En sus grupos, exploren otras ideas que se les ocurran.
Una vez que haya visto las 36 posibles combinaciones quizás
deba preguntarse "Me pregunto qué pasaría si …?" Haga un cambio
pequeño, explore qué pasa y compare con sus dos resultados.
Podría preguntarse ¿por qué …?
Este acertijo y su material de apoyo son una traducción; el original en inglés aparece en http://nrich.maths.org/6947
** Solo verás la sección "Notas para los Maestros" si has ingresado a la página como usuario registrado. Si eres maestro y quieres registrarte pulsa aquí. **
¿Qué patrones o relaciones has encontrado?
¿Por qué ocurren estas relaciones?
¿Qué pasa al rotar el cuadro chico/grande?
¿Qué pasa si se mueve el cuadrado chico/grande hacia arriba/abajo?
¡Publica tus resultados!
Si encontraste una solución, haz verificado que no tiene errores y estás orgulloso de ella, mándala por correo electrónico a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
junto con 1) tu nombre, 2) el nombre de tu escuela, 3) el nombre del acertijo.
Publicaremos las mejores soluciones que recibamos.
Puedes mandarla en cualquier formato. Si no te pueden ayudar a escribir tu respuesta en un archivo de computadora, puedes escanear tu trabajo original hecho en papel.
Aquí hay una versión imprimible del enunciado; van dos copias del mismo enunciado en una hoja carta.
En la sección de Enunciados Imprimibles hay juegos de enunciados sin repetir que se pueden imprimir.


