Rectas en el plano
Cada punto de un plano se puede describir por una pareja de números, (x, y).
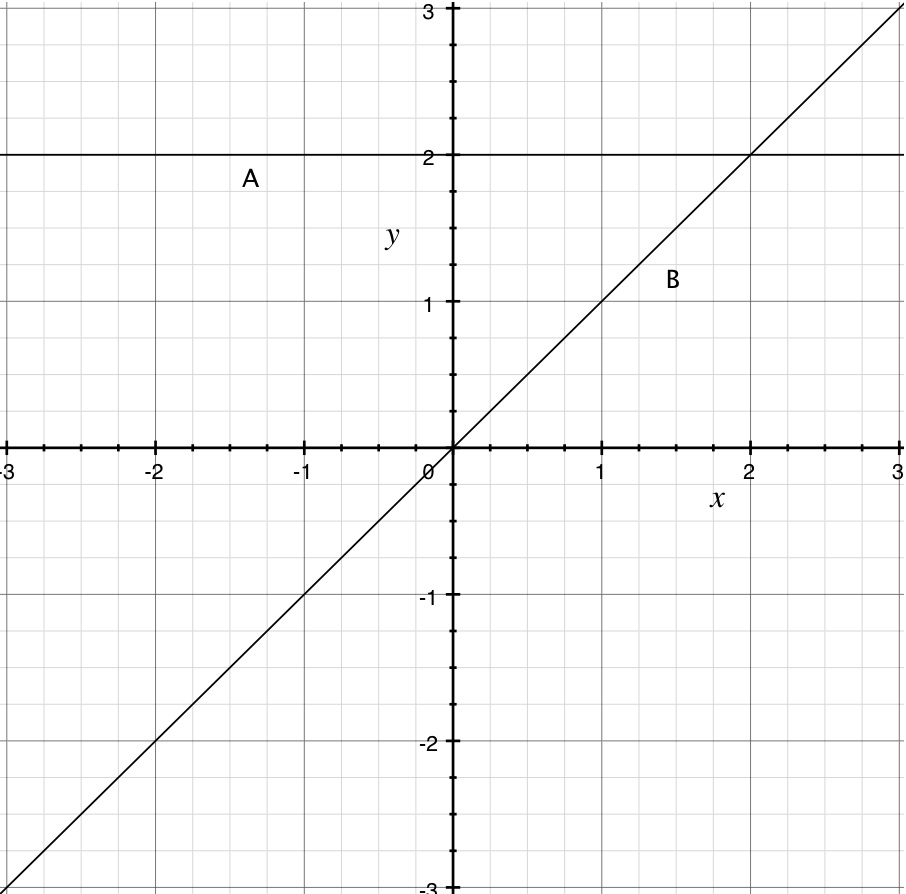
Observa que todos los puntos de la recta A, como el (0, 2) y el (1, 2) satisfacen la relación y=2. Además, si una pareja (x, y) tiene y = 2, entonces ese punto está en la recta A.
También verifica que los puntos de la recta B, como el (1, 1) y el (-2, -2), son los que satisfacen la ecuación y = x.
En la figura de abajo, ¿cuál es la recta y = x + 1/4? ¿Cuál es la recta y = x + 3? ¿Cuál es la recta y = 2x?

Usa la interactividad para relacionar distintas rectas y las relaciones (ecuaciones) que las caracterizan. Mueve el punto azul y el rojo para construir la recta caracterizada por la ecuación y= 3x + 2 . También construye las rectas y = -2x +1 , y = 2/3 x - 2
En este juego recolecta diamantes usando tu habilidad caracterizando rectas. Da la ecuación de tres rectas.
¡Todos los diamantes que tus rectas toquen serán tuyos!
Este acertijo utiliza partes de acertijos (en ingles) desarrollados por el proyecto NRICH: http://nrich.maths.org/5609 , http://nrich.maths.org/5725
** Solo verás la sección "Notas para los Maestros" si has ingresado a la página como usuario registrado. Si eres maestro y quieres registrarte pulsa aquí. **
Mientras usas la interactividad fíjate en la pareja de números (x, y) correspondiente a un punto de la recta. Verifica que esos números hacen que la ecuación sea válida.
¿Qué pasa a la recta cuando mueves el punto azul hacia arriba? y ¿qué le pasa a la ecuación?
¿Qué pasa a la recta cuando mueves el punto rojo hacia arriba? y ¿qué le pasa a la ecuación?
¡Publica tus resultados!
Si encontraste una solución, haz verificado que no tiene errores y estás orgulloso de ella, mándala por correo electrónico a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
junto con 1) tu nombre, 2) el nombre de tu escuela, 3) el nombre del acertijo.
Publicaremos las mejores soluciones que recibamos.
Puedes mandarla en cualquier formato. Si no te pueden ayudar a escribir tu respuesta en un archivo de computadora, puedes escanear tu trabajo original hecho en papel.
Aquí hay una versión imprimible del enunciado.
En la sección de Enunciados Imprimibles hay juegos de enunciados sin repetir que se pueden imprimir.


