Reflejando rectas
Aquí hay dos gráficas. Cada una muestra un par de líneas que son imágenes reflejadas una de la otra, una en el eje horizontal y otra en el eje vertical. 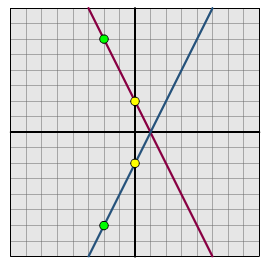

Mueve los puntos verdes y amarillos en la gráfica interactiva de abajo para crear algunos pares más de líneas reflejadas.
¿Qué puedes decir sobre las ecuaciones de dos líneas si una es la reflexión de la otra en el eje horizontal? ¿Qué pasa con si se refleja en el eje vertical?
A continuación se presentan las ecuaciones de dieciséis líneas rectas. Cada línea tiene asociada otra, ya sea su reflexión en el eje horizontal o en el vertical. Sin dibujar las gráficas, ¿puedes encontrar todos los pares y decir en qué eje se esta reflejando?

Ahora imagina que una recta es reflejada en uno de los ejes, después la imagen se refleja en el otro eje. ¿Puedes deducir la ecuación de la recta resultante si conoces la ecuación de la recta original? ¿Es distinto reflejar primero en el eje horizontal y luego en el vertical, o primero reflejar en el eje vertical y después en el horizontal? Explica tus resultados.
Este acertijo y su material de apoyo son una traducción; el original en inglés aparece en http://nrich.maths.org/6471
** Solo verás la sección "Notas para los Maestros" si has ingresado a la página como usuario registrado. Si eres maestro y quieres registrarte pulsa aquí. **
Es posible que quieras echar un vistazo a "Rectas en el plano" antes de trabajar en este problema.
¿Por qué no comenzar por la investigación de algunas ecuaciones cuyas gráficas se pueden visualizar fácilmente?
¡Publica tus resultados!
Si encontraste una solución, haz verificado que no tiene errores y estás orgulloso de ella, mándala por correo electrónico a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo.
junto con 1) tu nombre, 2) el nombre de tu escuela, 3) el nombre del acertijo.
Publicaremos las mejores soluciones que recibamos.
Puedes mandarla en cualquier formato. Si no te pueden ayudar a escribir tu respuesta en un archivo de computadora, puedes escanear tu trabajo original hecho en papel.
Aquí hay una versión imprimible del enunciado; van dos copias del mismo enunciado en una hoja carta.
En la sección de Enunciados Imprimibles hay juegos de enunciados sin repetir que se pueden imprimir.


