Club de Mate

Sucesiones de Farey

Si te dan una lista de números escritos como decimales, seguro te será fácil ordenarlos de acuerdo a su tamaño. Pero ¿cómo ordenas fracciones?

Un hombre llamado John Farey estudió sucesiones de fracciones con respecto a su tamaño; se llaman sucesiones de Farey.

La tercera sucesión de Farey, F₃, se ve así:

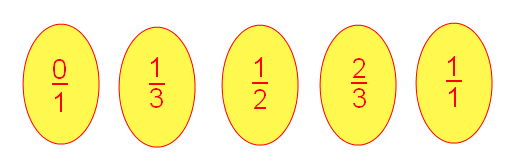
Esa sucesión en lista fracciones entre 0 y 1 con denominadores que llegan hasta 3,

incluyéndolo,  escritas en su forma más simple.

Te presentamos F₄:

Escribe tú F₅.

¿Cuáles fracciones extras aparecen en F₅ que no estaban en F₄?

Usa F₅ para ayudarte a completar F₆ y F₇.

Aquí hay algunas consideraciones.

Hay muchas fracciones extras en F₁₁que no aparecían en F₁₀.

Hay pocas fracciones extras en F₁₂ que no aparecían en F₁₁.

¿Puedes explicar por qué ocurre eso?

¿En qué casos necesitarás muchas fracciones extras para obtener la siguiente sucesión de Farey?

¿Será siempre una sucesión de Farey más larga que la anterior? ¿Cómo lo sabes?

Hasta ahora, todas las sucesiones de Farey han contenido un número impar de fracciones. ¿Puedes encontrar una sucesión de Farey con un número par de fracciones?

En F₄, 3/4 aparece entre 2/3 y 1/1. ¿Qué notas en las fracciones de ambos lados cuando colocas una nueva fracción?

Escoge cualesquiera tres fracciones consecutivas en una sucesión de Farey. ¿Puedes encontrar una forma de combinar las fracciones de los extremos para obtener la de en medio?

Para ver cómo se relacionan estas sucesiones con algunos patrones hermosos patrones matemáticos, vea los diagramas en el problema Círculos de Ford (en inglés). No es necesario intentar este último problema en este nivel, está dirigido a estudiantes de niveles más altos.

Este acertijo y su material de apoyo son una traducción; el original en inglés aparece en http://nrich.maths.org/2086